|
|
In het onderdeel Wiskundige hulpmiddelen nemen we diverse wiskundige begrippen onder de loupe.
Wiskunde is immers een nuttig instrument (maar ook niet meer dan dat) om allerlei fysische begrippen te beschrijven en voor te stellen.
Artikel 1: Dimensieloze functies
Artikel 2: Integralen met basic programma's
Artikel 3: Studie Fourier analyse
Artikel 4: Klasse-E-Versterker
|
Artikel 1: Dimensieloze functies |
Zonder het te beseffen is onze wiskunde opleiding volledig gebaseerd op het manipuleren van dimensieloze elementen.
Bijvoorbeeld in de algebraïsche functie y=ax+b zijn zowel x en y maar ook a en b abstracte dimensieloze getallen.
De verzoening tussen wiskunde en natuurkunde (elektronica) ligt juist in de transformatie van dimensieloze uitdrukkingen in zichtbare betekenisvolle elementen
zoals spoelen weerstanden en capaciteiten, en ook omgekeerd.
Raadpleeg het volledige artikel |
|
Artikel 2: Integralen met basic programma's |
In dit document wordt uitgelegd:
1) Hoe men toch een numerieke oplossing kan bekomen van gelijk welke integraal, zonder dat men integraal of differentiaal rekenen moet beheersen.
Sommige integralen zijn zelfs wiskundig niet op te lossen, maar numeriek wel!
2) Hoe men een grafiek kan bekomen welke het verloop van de integraal voorstelt, tussen de grenzen waarvan men de integraal wil oplossen.
3) Hoe men een generieke oplossing bekomt van alle integraal of differentiaal vergelijkingen van hogere orde. De oplossing wordt verwezenlijkt door VISUAL-BASIC programma’s.
Raadpleeg het volledige artikel |
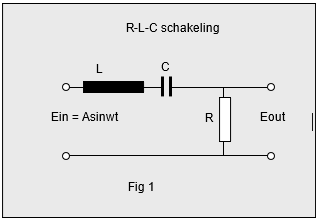 |
| Eenvoudig circuit - moeilijke wiskundige vergelijking |
|
Artikel 3: Studie Fourier analyse |
Voor ieder signaal dat digitaal kan gesampled worden en waarvan het aantal samples gedurende één periode een integer getal n is,
kan men uit de gesampelde waarden de verschillende amplitudes vinden van de verschillende harmonischen.
Deze (discrete) Fourier analyse, die niets meer is dan het oplossen van een matrix, wordt in dit artikel uitvoerig besproken.
Raadpleeg het volledige artikel |
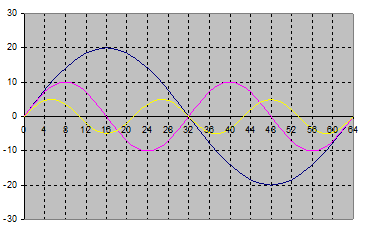 |
| Signaal met drie frequenties |
Artikel 4: Klasse-E-versterker
berekend met Algebra, Differentiaal, Laplace en Regeltechniek
|
Een eindtrap van een zender heeft tot doel om aan de antenne een wisselstroom en spanning te leveren om een bepaald vermogen te kunnen uitstralen in de lucht.
De wisselstroom en spanning zijn een Hoog-Frequent signaal (HF-signaal) in de orde van verschillende MegaHertz tot in de GigaHertz.
Om zo lang mogelijk met een batterij toe te komen, moet er voor gezorgd worden dat het rendement zo hoog mogelijk is of zo dicht mogelijk bij 100% ligt.
In dit artikel wordt een voorbeeld besproken met een eindtrap van een 2 Watt zender op 50 Mhz, gevoed vanuit een batterij van 9 volt,
en wordt ernaar gestreefd dit vermogen uit te zenden met een rendement van meer dan 90%.
|
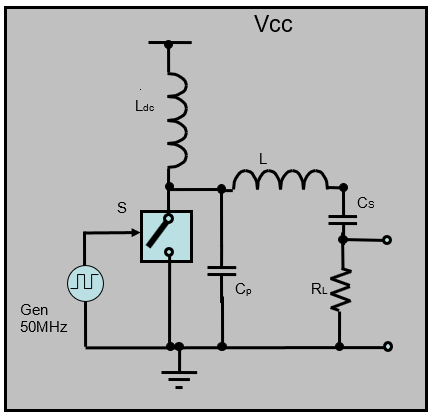 |
| Vermogen eindtrap |
In deze reeks van vier artikels wordt aangetoond dat de Klasse-E versterker op verschillende wetenschappelijke manieren of hulpmiddelen kan berekend worden
en allemaal tot hetzelfde resultaat leiden (mits een klein verschil in nauwkeurigheid).
Achtereenvolgend komen deze vijf wetenschappelijke methoden aan bod:
Algebra, Differentieel vergelijkingen, Laplace, Regeltechniek en Numeriek.
Raadpleeg de volledige artikels:
Klasse E versterker - Algebra
Klasse E versterker - Differentieel vergelijkingen
Klasse E versterker - Laplace
Klasse E versterker - Regeltechniek
Klasse E versterker - Numeriek
Terug naar boven op deze pagina
Terug naar de startpagina
|
|

